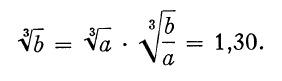|
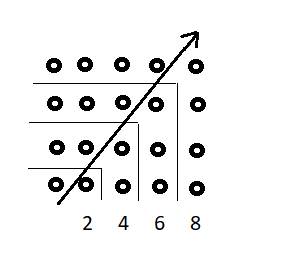
| Tablets da antiga Babilônia fornecem pistas sobre como era a matemática daquela região. As figuras ao lado
mostram a reprodução de um tablet com o cálculo da raíz cúbica. Os
pesquisadores Neugebauer e Sachs estimam que seja do ano 6295 a.C. Sua transcrição
e tradução para o inglês são também forneceidas pelos autores.
|

|
|
| Além do estilo
procedimental ("faça isso, depois isso") fica também aparente uma aproximação com o leitor. Não é uma expressão impessoal,
como a expressão matemática dos nossos dias. O trecho apresenta o cálculo da raíz cúbica de um dado número b = 3,22,30 (base sessenta). O autor explica que, para isso, é usado um número auxiliar
a = 7,30,0, cuja raíz cúbica igual a 30 é conhecida. Daí, segue-se o seguinte cálculo:
|

|
|
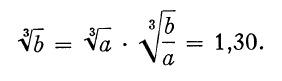 O cálculo pressupõe três condições: (1) que a seja o cubo de um número racional; (2) que a seja um número regular,
ou seja, pode ser decomposto em potências de 2,3 e 5, como 60 22 * 3 * 5;
(3) que a raíz cúbica de b/a possa ser calculada.
O cálculo pressupõe três condições: (1) que a seja o cubo de um número racional; (2) que a seja um número regular,
ou seja, pode ser decomposto em potências de 2,3 e 5, como 60 22 * 3 * 5;
(3) que a raíz cúbica de b/a possa ser calculada.
Fonte: Capítulo III de Mathematical Cuneiform Texts, que analisa diversos
exemplos da elaborada matemática babilônica.
|

|
|
|
|
|
|
|
Nos dias de hoje, após muitos séculos de um percurso matemático que se envergonha da aproximação com a vida e reivindica
para si o prestígio de um saber que se estabelece somente a nível do raciocínio apurado, presenciamos o testemunho
inconformado daqueles que buscam para a “Rainha das Ciências” uma origem fidalga. Estes, analisando o percurso das
matemáticas antigas, ainda esperam encontrar sinais de uma racionalidade não desvelada:
|
|
Os ensinamentos eram transmitidos na forma: ‘faça isso, depois isso, em seguida isso e esse é o resultado’. É difícil
acreditar que certas ‘receitas’ apresentadas pelos matemáticos babilônicos tenham sido descobertas apenas por tentativas,
sendo provável que algum raciocínio lógico, não explicitado, tenha sido usado
(Garbi 2007 p.12).
|
Outros textos famosos da atualidade, adotam uma concepção evolutiva cujo parâmetro é a
matemática praticada nos dias de hoje, ficando subjugado o atendimento às demandas de um povo em seu tempo e ambiente.
Nessa perspectiva, consideram como “deficiências da matemática” daquele tempo e lugar a falta de um raciocínio lógico
explícito e desvinculado das práticas. Uma matemática evoluída seria uma expressão abstrata, isto é, a expressão
descolada das coisas do mundo que lhe serviram de inspiração:
|
|
Os papiros e tabletas encontrados contém apenas casos específicos e problemas, sem
formulações gerais, e pode-se perguntar se essas civilizações antigas realmente percebiam os princípios unificadores
que estão no centro da matemática
(Boyer 1999 p.28).
|
São muitas as evidências de que o conhecimento matemático não tem suas origens no mais nobre
intelecto por meio do raciocínio lógico, ao contrário, essas histórias antigas mostram que estava, desde sempre, na feira,
no comércio, na agricultura, na fé, para resolver questões imediatas da vida e da busca humana por explicações diante de
sua finitude. Esses ambientes turbulentos permitiram uma confluência de fatores que estimularam o pensamento de modo a
criar as mais diversas expressões e soluções. Sob este ponto de vista, a matemática de ‘receitas’ é suficientemente evoluída,
a ponto de resolver as demandas do seu tempo e local.
|
|
|